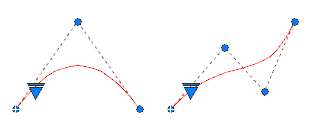
Spline, eğrinin şeklini etkileyen bir dizi noktadan geçen veya bu noktalara yakın geçen düzgün bir eğridir.
Varsayılan olarak, bir spline, 3. derece (kübik olarak da adlandırılan) polinomların birleştirilmiş eğri segmentlerinden oluşan bir seridir. Bu eğriler teknik olarak düzensiz rasyonel B-spline’lar (NURBS) olarak adlandırılır , ancak basitlik açısından spline olarak anılırlar. Kübik spline’lar en yaygın olanıdır ve veri noktalarındaki ağırlıklarla şekillendirilen esnek şeritler kullanılarak elle oluşturulan spline’ları taklit eder.
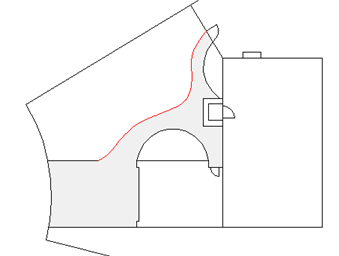
Aşağıdaki örnekte, beton kaldırımın vurgulanan sınırını oluşturmak için bir spline eğrisi kullanılmıştır.
Kontrol Noktalarını ve Uyum Noktalarını Anlamak #
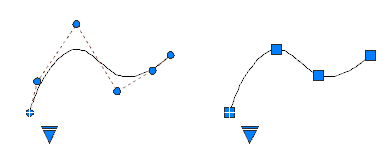
Kontrol noktaları veya uyum noktaları kullanarak eğriler oluşturabilir veya düzenleyebilirsiniz . Soldaki eğri, bir kontrol çokgeni boyunca kontrol noktalarını , sağdaki eğri ise uyum noktalarını göstermektedir.
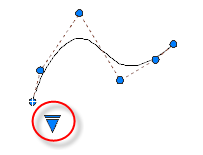
Seçili bir eğri üzerinde üçgen tutamacı kullanarak kontrol noktaları ve uyum noktaları arasında geçiş yapabilirsiniz. Yuvarlak ve kare tutamaçları kullanarak seçili bir eğriyi değiştirebilirsiniz.
Uygun Noktaları Kullanarak Eğriler Oluşturun #
Uygun noktalar kullanarak spline eğrileri oluşturduğunuzda, ortaya çıkan eğri belirtilen noktalardan geçer ve eğrideki matematiksel düğümlerin aralığından etkilenir .
Düğüm parametreleştirme seçeneğiyle bu düğümlerin aralığını seçebilirsiniz ; bu da örnekte gösterildiği gibi farklı eğriler elde etmenizi sağlayacaktır.
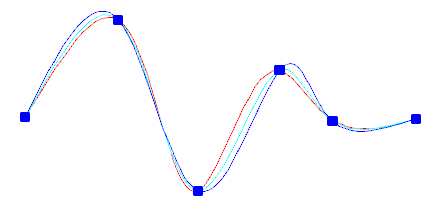
Tolerans değeri 0 olarak ayarlandığında, eğri doğrudan uyum noktalarından geçer. Daha büyük tolerans değerlerinde ise eğri uyum noktalarına yakın bir yerden geçer. İsteğe bağlı olarak, eğrinin her iki ucundaki teğet yönünü belirtebilirsiniz.
Özel Durumlar #
Soldaki resimde gösterildiği gibi, tam olarak 3 kontrol noktasıyla oluşturulmuş 2. derece bir spline belirterek parabolik şekilli bir spline oluşturabilirsiniz. Sağdaki resimde gösterildiği gibi, 4 kontrol noktasıyla oluşturulmuş 3. derece spline’lar, 3. derece Bezier eğrileriyle aynı şekle sahiptir.