HI Solver’ın temel gereksinimi, çözümün geçmişten bağımsız olmasıdır: çözüm, yalnızca hedef ve diğer tesadüfi parametrelerin mevcut durumlarına dayanmalıdır.
Dönme Açısı Serbestlik Derecesi #
Tek bir zincir için konum hedefi verildiğinde, açık bir serbestlik derecesi kalır: Uç Etkileyici Eksen (EE Ekseni) etrafındaki dönüş. Dönme açısı, bu serbestlik derecesini niceliksel olarak tanımlamak için kullanılır.
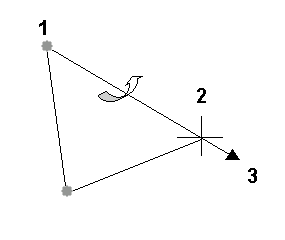
1. Eklemi başlatın.
2. Uç efektör
3. EE ekseni
Çözücü Düzlemi #
Tüm eklemlerden geçen düzleme Çözüm Düzlemi diyelim. Eklemler bir düzlem üzerinde yer almadığında, bu düzlemi (A) Başlangıç Eklemi ve Bitiş Eklemi’nden geçen ve (B) belirli bir anlamda kalan ekleme en yakın olan düzlem olarak tanımlayacağız.
Dönme Açısı, Çözücü Düzleminin serbestlik derecesini tanımlar ve yalnızca Başlangıç Eklemini kısıtlar.
Sıfır Düzlemi Haritası #
Çözücü düzlemini sayısal bir değerle tanımlayabilmek için, 0’ın ne anlama geldiği konusunda hemfikir olmalıyız. Uç efektör pozisyonu verildiğinde, Sıfır (Çözücü) Düzlemi nerededir? Sıfır Düzlem Haritası, argüman olarak EE Eksenini alır ve sıfır düzlemine dik olan normali üretir.
Ters kinematik (IK) sistemi, her bir çözücü eklentisinin kendi Sıfır Düzlem Haritalarını tanımlamasına olanak tanır. Tanımlanmadığında, IK sistemi varsayılan bir harita sağlar.
Sıfır Düzlem Haritası’nın argümanı, EE ekseninin yönünü veren birim vektördür. Eşdeğer olarak, EE, EE ekseni boyunca kaydığında, çözücü düzlemi sabit kalmalıdır. Bu nedenle, Sıfır Düzlem Haritası bir küre üzerinde bir vektör alanı tanımlar. Küre üzerindeki bir nokta verildiğinde, sıfır düzlemine dik olarak yorumlanacak bir teğetsel birim vektör üretir.
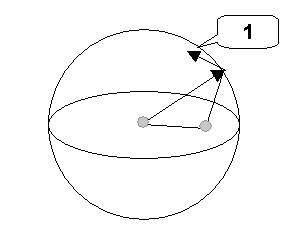
1. Sıfır düzlemine dik
Çözücü Düzlem Çevirme #
Bir küre üzerinde sürekli bir vektör alanının bulunmadığı matematiksel bir gerçektir. Ne kadar uğraşırsanız uğraşın, küre üzerinde komşu vektörlerin önemli ölçüde değiştiği bir nokta her zaman olacaktır. Uç efektör ekseni bu noktaya yaklaştığında çözücü düzlemi bu noktada ters dönecektir.
Çünkü bir yandan, tarihten bağımsız olma gerekliliği, tekil noktaya sabit bir vektör atamamızı gerektirirken, diğer yandan, hangi vektör atanırsa atansın, komşu noktalara atanan bazı vektörlerden önemli ölçüde farklı olacaktır.
Kürenin İçsel Referans Çerçevesi #
Sıfır Düzlem Haritasını tanımlamak için, küre için bir referans çerçevesi tanımlamamız gerekir. Bu referans çerçevesi, eklem zincirinin kendisine özgüdür.
Bir küre, merkez, yatay düzlem ve meridyen (sıfır boylam) ile tanımlanabilir. Merkez, başlangıç eklemine atanır.
Tüm eklem açılarının tercih edilen açıları aldığı pozisyon özellikle önemlidir. Buna tercih edilen pozisyon diyelim.
Tercih edilen pozisyondaki çözüm düzlemini yatay düzlem olarak kullanıyoruz. Dönme açısı başlangıç eklemini kontrol etmek için kullanıldığından, başlangıç eklemindeki tercih edilen açılar o kadar da içsel değildir. Başlangıç eklemine sıfırlar ve diğer eklemlere tercih edilen açılar atanarak elde edilen çözüm düzlemiyle yatay düzlemi tanımlamak da mantıklıdır.
EE ekseni meridyeni tanımlar. Küre artık aşağıdaki şekilde gösterildiği gibi tanımlanmıştır:
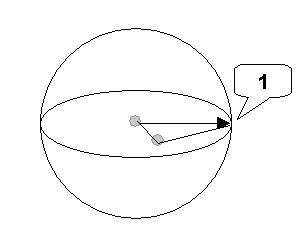
1. EE ekseni
Tüm eklemler tercih edilen açıları alır. Sıfır Düzlem Haritası bu küre üzerinde tanımlanacaktır.
Eklenti çözücüsünün kendi Sıfır Düzlem Haritasını tanımlaması için kullanılan API, aslında EE eksenini ve tercih edilen pozisyondaki çözücü düzlemine dik olan normali alır:
sanal sabit IKSys::ZeroPlaneMap* GetZeroPlaneMap(const Point3& a0, sabit Point3& n0) sabit
Burada a0 ve n0 sırasıyla tercih edilen pozisyondaki EE ekseni ve çözüm düzlemidir. ZeroPlaneMap nesnesi, küre üzerindeki her noktaya bir düzlem normali atayan bir fonksiyondur.
Varsayılan Sıfır Düzlem Haritası #
Eklenti çözücüler tarafından sağlanmadığında (IK Çözücü’nün kendisi bir eklenti çözücü olarak uygulanmıştır), IK sistemi varsayılan bir tane sağlayacaktır. Bu harita aşağıdaki kurallarla tanımlanır:
- A: Ekvator üzerindeki her nokta için, yatay düzlem ile kürenin kesişim noktasında, normal vektör, tercih edilen pozisyondaki çözücü düzleminin normaliyle aynı yöne işaret eden dikey vektör olarak tanımlanır.
- B: Kuzey ve güney kutupları dışındaki küre üzerindeki herhangi bir nokta için, o noktadan ve kuzey, güney kutuplarından geçen bir büyük çember vardır. Bu çember ekvatoru iki noktada keser. Bu noktalardan biri verilen noktaya daha yakındır. Verilen noktadaki normal vektör, ekvator üzerindeki daha yakın noktadaki normalin, büyük çember boyunca teğetsel olarak hareket ettirilmesiyle elde edilir.
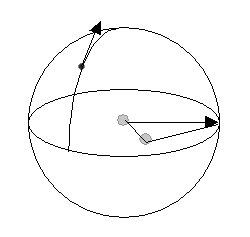
Sıfır düzlemine ait varsayılan normalin türetilmesi
Açıkçası, bu yöntem kuzey veya güney kutuplarına uygulanamaz. Bunlar tekil noktalardır. EE ekseni kutuplar boyunca hareket ettiğinde, normal aniden yön değiştirir: kullanıcıların bakış açısından tersine döner.
Normalde, tercih edilen pozisyon, çözücüye ilk atama yapıldığı pozisyondur. Dolayısıyla, eklemlerin yerleştirildiği düzlem, buradaki yatay düzleme karşılık gelir. A kuralı, hedef düzlem üzerinde hareket ettirilirse zincirin düzlem üzerinde kalmasını sağlar.
B kuralı, hedefi büyük daire boyunca ekvatora dik olarak hareket ettirdiğinizde, zincirin kutuplardan geçmediği sürece dikey kalacağı anlamına gelir; kutuplar bu haritanın tekil noktalarıdır.
Ebeveyn Alanı #
Şimdiye kadar, tüm dünyanın yalnızca ters kinematik (IK) unsurlardan oluştuğu varsayımıyla her şeyi tanımladık. Pratikte, IK zinciri ve hedefi ayrı dönüşüm hiyerarşilerinin noktalarında yer alabilir. Sonuç olarak, dünyada tanımlanan uç efektörün konumunu küre üzerindeki bir noktaya eşlememiz gerekiyor. Kürenin uç efektör konumuna göre nasıl monte edildiğine bağlı olarak, enlem ve boylam okumaları farklıdır. Bu kürenin yerleştirileceği ana dönüşüm uzayına, bağlam açık olduğunda Döndürme Açısı Ana Uzayı veya Ana Uzay denir.
Ana uzay, IK parametrelerine göre değişmez olmalıdır. Şu anda iki seçenek sunuyoruz:
- Başlangıç Eklemi Dönme Açısı Üst Alanı, Başlangıç Ekleminin üst alanı ile aynıdır.
- IK Hedefi Döndürme Açısı Üst Alanı, IK Hedefinin üst alanıdır.
Örnek 1 #
Başlangıç eklemi ve hedef doğrudan dünyaya bağlıysa, Ebeveyn Alanı seçimi herhangi bir fark yaratmaz. Aşağıdaki örnekte, başlangıç eklemi A nesnesine bağlıdır.
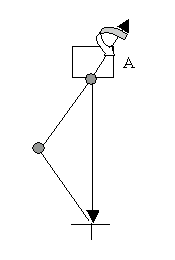
Ters kinematik zincir, başlangıç eklemi aracılığıyla A nesnesine bağlanır.
IK çözücüsü atandığında pozisyonun bu olduğunu varsayalım. Dolayısıyla, bu tercih edilen pozisyondur. Eklemlerin yerleştirildiği düzlem, (Sıfır Düzlem Haritası) küresinin yatay düzlemidir.
- A: Ebeveyn Alanı Başlangıç Eklemi’dir. Bu durumda, küre A’ya ebeveyn olarak bağlanmıştır. A çizilen eksen etrafında döndürülürse, küre de onunla birlikte döner. Hedef ayrı bir dönüşüm hiyerarşisindedir. Yerinde kalır ve IK çözümü nedeniyle uç efektör ona yapışır. (Düzlem) normali küreye sabitlendiğinden, o da A ile birlikte döner. Bu nedenle, tüm zincir ebeveyn nesneyle birlikte dönmüş gibi görünür.
- B: Ebeveyn Uzayı, Ters Kinematik Hedeftir. Hedefin dünyaya bağlı olduğunu varsayalım. Bu durumda, küre dünyaya bağlıdır ve bu nedenle sabit kalır. Normal küreye sabitlendiğinden, A döndürüldüğünde zincir sabit görünecektir.
Örnek 2 #
Aşağıdaki örnekte, ters kinematik çözücü atandığında ana uzayda bir dönüşün mevcut olduğu bir durumu inceliyoruz.
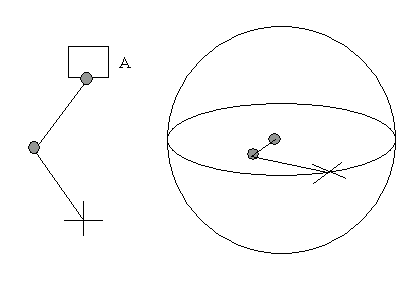
IK çözücüsü atandığında, IK zincirinin ana uzayı bir dönüş içerir.
A ana nesnesi 90 derecelik bir dönüş içerir. Bu , kullanıcının IK çözücüsü olmadan dört kemik oluşturduğu ve daha sonra Bone2’den Bone4’e bir IK çözücüsü atadığı durumun soyut bir temsilidir . Zinciri doğrudan dünyaya bağlarsak, sağdaki şekilde gösterildiği gibi görünür: çözücü düzlemi yatay hale gelir.
- A: Ana Uzay, Başlangıç Eklemi’dir. Küre, A’nın döndürülmesinden sonra monte edilir ve bu nedenle “yatay düzlem”, görünüm penceresinde gösterildiği gibi zincir düzlemiyle çakışır. Tekil noktalar, düzleme göre Başlangıç Eklemi’ne diktir. Hedef/uç efektör düzlem üzerinde hareket ettirildiğinde, asla tekil noktalara çarpmaz ve ters dönmez.
- B: Ana Uzay, Ters Kinetik Hedeftir. Yine, hedefin ana uzayının dünya olduğunu varsayıyoruz. Kürenin “yatay düzlemi”, sağdaki şekilde gösterildiği gibi yatay hale gelir. Tekil noktalar, kutuplar, eklemlerin yerleştirildiği düzlem üzerindedir. Bu nedenle, kullanıcılar hedefi/uç efektörü soldan sağa veya tam tersi yönde hareket ettirdiğinde, uç efektör tekil noktanın üzerinden geçerek ters dönecektir.
B seçeneğinin sorunlarından biri, sağdaki şeklin kullanıcıya asla gösterilmemesidir. Kullanıcı, çevirme işlemini anlamak için bu şekli zihninde canlandırmak zorundadır.
Örnek 3 #
Bu örnek, Başlangıç Eklemi yeniden atandığında neler olduğunu açıklamaktadır. Dört kemik düğümünden oluşan bir IK zincirimiz olduğunu varsayalım.
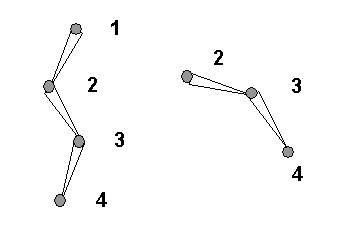
1. Kemik01
2. Kemik02
3. Kemik03
4. Kemik04
Başlangıç ve bitiş eklemleri sırasıyla Bone01 ve Bone04’tür . Şekilde gösterilen pozun tercih edilen poz olduğunu ve Bone01’in bir dönüş içerdiğini varsayalım. Bone02’yi doğrudan dünyaya bağlarsak , Bone02’den gelen hiyerarşi sağdaki şekilde görünecektir.
Başlangıç Eklemini Bone02’ye yeniden atadığımızda , Sıfır Düzlem Haritası küresi sağdaki yapılandırmaya göre oluşturulacaktır.
- A: Ebeveyn Alanı Başlangıç Eklemi’dir. Bu durumda, sağ konfigürasyona sabitlenmiş küre, Bone01 ile birlikte ebeveyn olarak bağlanmalıdır. Bu , Bone01’den Bone04’e olanla aynı olacaktır . Bu nedenle, aynı normali elde ederiz ve zincir sabit kalır.
- B: Ebeveyn Alanı, Ters Kinetik Hedeftir. Bu durumda, küre dünyada kalırken Bone02 , Bone01’e ebeveyn olarak bağlanmıştır . Bone01’in dönüşümü nedeniyle Bone04 solda gösterilen yere taşındığında , dünyaya sabitlenmiş küreye sabitlenmiş gözlemci, Bone04’ün tercih edilen poz tarafından tanımlanan nötr konumdan uzaklaştığını görecektir. Algoritma daha sonra yer değiştirmiş konumdaki normali bulmak için Sıfır Düzlem Haritasını uygular. Genellikle görüş alanına dik değildir. Bu nedenle, yeni bir Başlangıç Eklemi aldığında bir ters çevirme göreceğiz.
Çözücü/hedefi silip Bone02’den Bone04’e yeni bir tane atarsanız , zincirin ters dönmediğini göreceksiniz. Neden? Başlangıç Eklemi ataması, yeni bir IK zinciri/hedefi oluşturmaktan farklıdır. Başlangıç Eklemi, birçok IK parametresinden biridir. Yeniden atamak, herhangi bir parametreyi değiştirmekle aynıdır. Diğer parametreler olduğu gibi kalır. Özellikle, bu yeniden atama sonucunda Dönme Açısı değişmez.
Yeni bir IK zinciri/hedefi oluşturmak farklıdır. Eklem zincirinin sabit kalması için parametreler uygun şekilde ayarlanarak çaba sarf edilir. Özellikle, çözücü düzleminin görüntü alanında sabit kalmasını sağlayacak bir değere Döndürme Açısı ayarlanır.




