NURBS eğrileri ve yüzeyleri geleneksel teknik çizim dünyasında mevcut değildi. Bunlar, bilgisayarlar kullanılarak 3 boyutlu modelleme için özel olarak oluşturulmuştur. Eğriler ve yüzeyler, 3 boyutlu modelleme alanında konturları veya şekilleri temsil eder. Matematiksel olarak oluşturulurlar.
NURBS matematiği karmaşıktır ve bu bölüm, oluşturduğunuz şeyi ve NURBS nesnelerinin neden böyle davrandığını anlamanıza yardımcı olabilecek bazı NURBS kavramlarına basit bir giriş niteliğindedir. NURBS modellemesinde kullanılan matematik ve algoritmaların kapsamlı bir açıklaması için Les Piegl ve Wayne Tiller’ın yazdığı “The NURBS Book” (New York: Springer, ikinci baskı 1997) kitabına bakabilirsiniz.
Tanım ve Parametre Alanı #
NURBS terimi , Düzensiz Rasyonel B-Eğrileri anlamına gelir . Spesifik olarak:
- Düzensiz dağılım, bir kontrol noktasının etkisinin kapsamının değişebileceği anlamına gelir. Bu, düzensiz yüzeyleri modellemede faydalıdır.
- Rasyonel, eğriyi veya yüzeyi temsil etmek için kullanılan denklemin, tek bir toplam polinom yerine iki polinomun oranı olarak ifade edilmesi anlamına gelir. Rasyonel denklem, özellikle konik kesitler, koniler, küreler vb. gibi bazı önemli eğriler ve yüzeyler için daha iyi bir model sağlar.
- B -spline ( temel spline) üç veya daha fazla nokta arasında enterpolasyon yapılarak bir eğri oluşturma yöntemidir.
Çizgi aracı ve diğer Şekil araçları gibi şekil eğrileri, B-spline’ların özel bir durumu olan Bezier eğrileridir.
NURBS’nin tekdüze olmayan özelliği önemli bir noktayı gündeme getiriyor. Matematiksel olarak üretildikleri için, NURBS nesneleri, görüntülendikleri 3 boyutlu geometrik uzaya ek olarak bir parametre uzayına da sahiptir. Özellikle, düğümler adı verilen bir değer dizisi, her bir kontrol noktasının (CV) eğri veya yüzey üzerindeki etki derecesini belirtir. Düğümler 3 boyutlu uzayda görünmezdir ve doğrudan manipüle edilemezler, ancak bazen davranışları NURBS nesnesinin görünür görünümünü etkiler. Bu konu bu durumları ele almaktadır. Parametre uzayı, 3 boyutlu uzayda geometrik olarak var olsalar bile, topolojik olarak yalnızca tek bir U boyutuna sahip olan eğriler için tek boyutludur. Yüzeyler, parametre uzayında U ve V olarak adlandırılan iki boyuta sahiptir.
NURBS eğrileri ve yüzeyleri, standart geometrik afin dönüşümler (Dönüşümler) veya perspektif projeksiyonlar altında değişmeme gibi önemli özelliklere sahiptir. Kontrol noktaları (CV’ler) nesnenin yerel kontrolünü sağlar: bir CV’yi hareket ettirmek veya ağırlığını değiştirmek, komşu CV’lerin ötesindeki nesnenin hiçbir bölümünü etkilemez. (Bu özelliği Yumuşak Seçim kontrollerini kullanarak geçersiz kılabilirsiniz.) Ayrıca, CV’leri birbirine bağlayan kontrol kafesi yüzeyi çevreler. Bu, dışbükey zarf özelliği olarak bilinir.
Derece ve Süreklilik #
Tüm eğrilerin bir derecesi vardır. Bir eğrinin derecesi, onu temsil etmek için kullanılan denklemdeki en yüksek üs değeridir. Doğrusal bir denklem 1. derecedendir; ikinci dereceden bir denklem 2. derecedendir. NURBS eğrileri tipik olarak kübik denklemlerle temsil edilir ve 3. derecedendir. Daha yüksek dereceler mümkündür, ancak genellikle gereksizdir.
Eğrilerin de sürekliliği vardır. Sürekli bir eğri kesintisizdir. Sürekliliğin farklı seviyeleri vardır. Açısı veya sivri ucu olan bir eğri C0 süreklidir : yani, eğri süreklidir ancak sivri uçta türevi yoktur. Böyle bir sivri ucu olmayan ancak eğriliği değişen bir eğri C1 süreklidir . Türevi de süreklidir, ancak ikinci türevi sürekli değildir. Kesintisiz, değişmeyen bir eğrilik C2 süreklidir . Hem birinci hem de ikinci türevleri de süreklidir.

Eğri sürekliliğinin seviyeleri:
Sol: C 0 , üstteki açı nedeniyle
Ortada: C 1 , üstte bir yarım daire, daha küçük yarıçaplı bir yarım daireye bağlanır.
Sağ: C 2 , fark ince ama sağ taraf yarım daire şeklinde değil ve sol tarafla bütünleşiyor.
Bir eğri daha yüksek süreklilik seviyelerine de sahip olabilir, ancak bilgisayar modellemesi için bu üçü yeterlidir. Genellikle göz, C2 sürekli bir eğri ile daha yüksek sürekliliğe sahip bir eğriyi ayırt edemez .
Süreklilik ve derece birbiriyle ilişkilidir. 3. dereceden bir denklem, C2 sürekli bir eğri üretebilir . Bu nedenle, NURBS modellemesinde genellikle daha yüksek dereceli eğrilere ihtiyaç duyulmaz. Daha yüksek dereceli eğriler sayısal olarak daha az kararlıdır, bu nedenle kullanılmaları önerilmez.
NURBS eğrisinin farklı bölümleri farklı süreklilik seviyelerine sahip olabilir. Özellikle, kontrol noktalarını aynı yere veya birbirine çok yakın yerleştirerek süreklilik seviyesini azaltırsınız. Çakışan iki kontrol noktası eğriliği keskinleştirir. Çakışan üç kontrol noktası eğride açılı bir sivri uç oluşturur. NURBS eğrilerinin bu özelliği çokluk olarak bilinir. Aslında, eklenen bir veya iki kontrol noktası, eğrinin o bölgesinde etkilerini birleştirir.
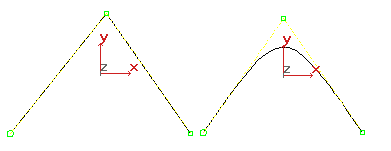
Çokluluğun etkileri: Soldaki tepe noktasında üç, sağdaki tepe noktasında ise iki kontrol grubu (CV) bulunmaktadır.
Bir kontrol noktasını diğerinden uzaklaştırarak, eğrinin süreklilik seviyesini tekrar artırırsınız. Kontrol noktalarını birleştirdiğinizde de çokluk etkisi geçerlidir. Birleştirilmiş kontrol noktaları, eğride daha keskin bir eğrilik veya sivri bir nokta oluşturur. Yine, kontrol noktalarını ayırıp birini diğerinden uzaklaştırdığınızda bu etki ortadan kalkar.
Derece, süreklilik ve çokluk kavramları, eğriler gibi NURBS yüzeyleri için de geçerlidir.
Eğrilerin ve Yüzeylerin İyileştirilmesi #
Bir NURBS eğrisini iyileştirmek, daha fazla kontrol noktası (CV) eklemek anlamına gelir. İyileştirme, eğrinin şekli üzerinde daha hassas kontrol sağlar. Bir NURBS eğrisini iyileştirdiğinizde, 3ds Max orijinal eğriliği korur. Başka bir deyişle, eğrinin şekli değişmez, ancak komşu kontrol noktaları eklediğiniz kontrol noktasından uzaklaşır . Bunun nedeni çokluktur: eğer komşu kontrol noktaları hareket etmeseydi, kontrol noktalarının artan varlığı eğriyi daha keskin hale getirirdi. Bu etkiden kaçınmak için, önce eğriyi iyileştirin ve ardından yeni eklenen kontrol noktalarını dönüştürerek veya ağırlıklarını ayarlayarak değiştirin.
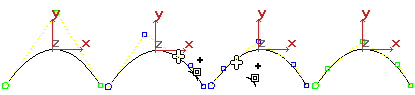
NURBS eğrisinin iyileştirilmesi.
NURBS yüzeyleri, temelde NURBS eğrileriyle aynı özelliklere sahiptir, ancak tek boyutlu bir parametre uzayından iki boyuta genişletilmiştir.
CV Eğrilerinin ve Yüzeylerinin Yeniden Parametrelendirilmesi #
Bir NURBS eğrisini veya yüzeyini iyileştirirken, yeniden parametrelendirmek iyi bir fikirdir. Yeniden parametrelendirme, eğri veya yüzeyin görünüm pencerelerinde düzenlendiğinde düzgün davranması için parametre alanını ayarlar. Yeniden parametrelendirmenin iki yolu vardır:
- Akor uzunluğu
Kiriş uzunluğuna dayalı yeniden parametrelendirme, parametre uzayındaki düğüm noktalarını her eğri parçasının uzunluğunun kareköküne göre düzenler.
- Üniforma
Tekdüze yeniden parametrelendirme, düğümleri tekdüze şekilde dağıtır. Tekdüze bir düğüm vektörünün avantajı, düzenleme yapıldığında eğrinin veya yüzeyin yalnızca yerel olarak değişmesidir.
CV eğrisi ve yüzey alt nesneleri, eğriyi veya yüzeyi düzenlediğinizde otomatik olarak yeniden parametrelendirme seçeneği sunar.
Nokta, Eğri ve Yüzey Kavramları #
Noktasal eğriler ve noktasal yüzeylerin yanı sıra CV eğrileri ve yüzeyleriyle de çalışabilirsiniz. Bu nesneleri kontrol eden noktalar, eğri veya yüzey üzerinde yer almakla sınırlıdır . Kontrol kafesi veya ağırlık kontrolü yoktur. Bu, çalışmayı daha kolay bulabileceğiniz daha basit bir arayüzdür. Ayrıca, nokta tabanlı nesneler, bağımlı (sınırlı) noktalara dayalı eğriler oluşturmanıza ve ardından bunları bağımlı yüzeyler oluşturmak için kullanmanıza olanak tanır.
Nokta eğrilerini ve yüzeylerini, tam olarak tanımlanmış NURBS nesneleri olan kontrol noktası eğrileri ve yüzeylerine bir arayüz olarak düşünebilirsiniz. Eğrinin veya yüzeyin temel temsili hala kontrol noktaları kullanılarak oluşturulmaktadır.
Nokta eğrisini veya yüzeyini noktalarına bağlı olarak da düşünebilirsiniz. Nokta eğrisini veya yüzeyi CV biçimine dönüştürmek veya tam tersini yapmak için Eğriyi Dönüştür düğmesini kullanabilirsiniz.




